【数据挖掘算法分享】机器学习平台——回归算法之逻辑回归算法大数据行业资讯-美林数据

产品简介

美林新闻/NEWS

首页美林数据行业资讯

【数据挖掘算法分享】机器学习平台——回归算法之逻辑回归算法

2022-12-13 19:13:08 次

逻辑回归算法可用于二元及多元分类问题，是分类算法的经典算法。对于二分类问题，算法输出一个二元Logistic回归模型。对于K分类问题，算法会输出一个多维Logistic回归模型，包含K-1个二分类模型。
►算法思想
逻辑回归在线性回归的基础上，套用了一个Sigmoid函数。逻辑回归名为回归，但实际上一般用于二分类。因为，其回归预测范围为[0,1]时，很符合概率特性。故对一个二分类问题，如果将正类定义为1，负类定义为0时，用逻辑回归结果代表样本属于正类的的概率，则预测值接近于0时，表示样本属于正类的概率很小，样本可被分到负类；反之，预测值接近于1时，样本被分到正类。
分类问题中，分类边界可以归纳为如下形式：

其对应的预测函数为：

二分类逻辑回归算法整体步骤如下：
逻辑回归二分类的步骤如下：
（1）构造单个样本的概率预测函数

：

其中的

为系数向量θ的常数项；θ_i为第i个自变量x_i的系数。
（2）对函数h_θ (x)的值赋予以下含义：它表示分类变量y取1的概率。因此对于输入的自变量向量x，分类结果为类别1和类别0的概率分别为：

（3）对于含有m个样本的训练集，构造其概率密度似然函数：

则其对数似然函数为：

（4）对于m个样本，通过梯度下降法求出使对数似然函数

取得最大值的系数向量 θ 的估计值

。
（5）令

，使用概率计算公式，分别计算出每个样本属于类别1和类别0的概率。
（6）依据事先给定的概率阈值

（通常为0.5），对每个样本属于两类的概率进行截取，进而得到样本的所属类别。
二元逻辑回归可以一般化为多元逻辑回归来训练和预测多分类问题。对于多分类问题，算法将会训练出一个多元逻辑回归模型，它包含k-1个二元回归模型。给定一个数据点，k-1个模型都会运行，概率最大的类别将会被选为预测类别。

►数据格式
• 必须设置类属性（输出），且类属性（输出）必须是离散型（名词）；
• 非类属性（输入）可以是连续型（数值）也可以是离散型（名词）；
►参数说明

参数	类型	描述
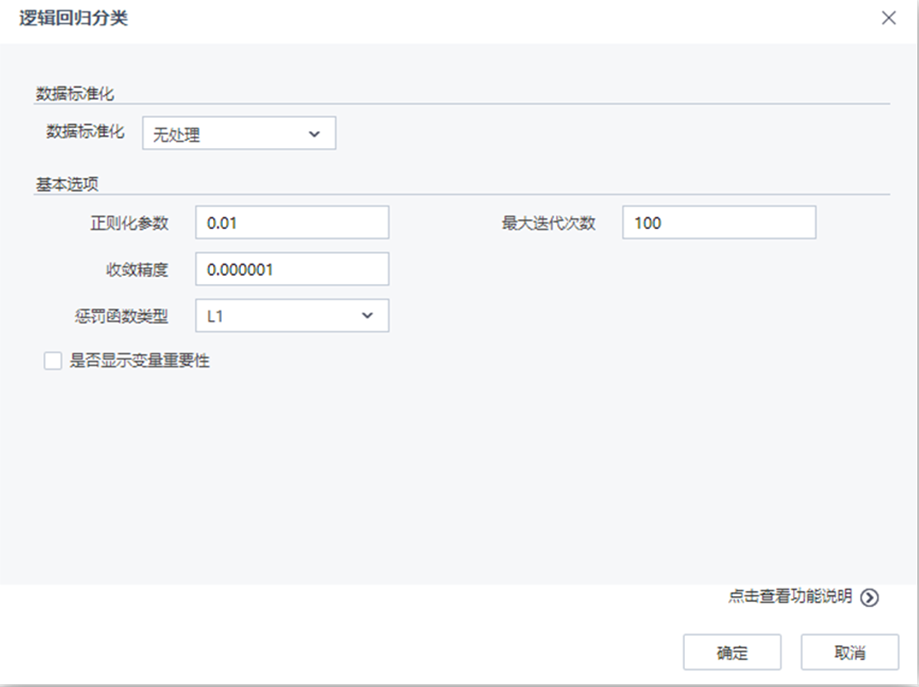
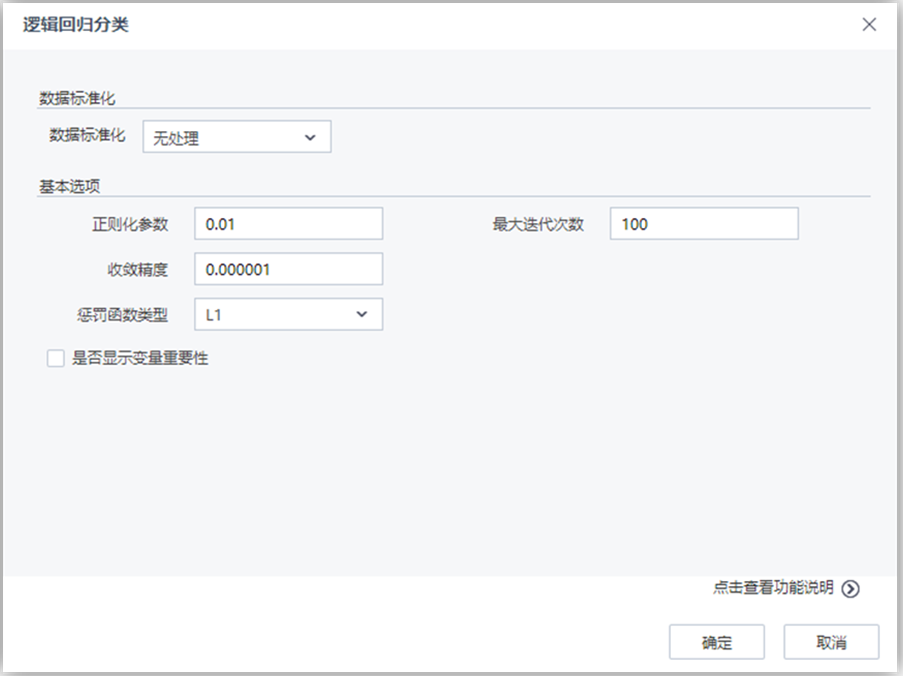
数据标准化	下拉框	设置数据标准化的方法，字符型，取值范围：无处理，归一化，标准化，默认值为无处理
取值区间下限	文本框	设置归一化取值区间下限，浮点型，取值范围：[0,∞)，默认值为0
取值区间上限	文本框	设置归一化取值区间上限，浮点型，取值范围：[0,∞)，默认值为1
正则化参数	文本框	正则化参数控制机器的复杂度，浮点型，取值范围：[0,∞)，默认值为0.01
收敛容差	文本框	设置终止迭代的误差界，浮点型，取值范围：[0,∞)，默认值为0.000001
最大迭代次数	文本框	设置最大迭代次数，整型，取值范围：[1,∞)，默认值为100
惩罚函数类型	下拉框	设置惩罚函数类型，0对应L2罚函数，1对应L1罚函数，(0,1)之间对应L1和L2的组合罚函数，浮点型，取值范围：[0,1]，默认值为0
是否显示变量重要性	复选框	用户选择是否分析每个变量对于分类结果的影响程度，如果选择是，则在洞察中显示参与建模的每个变量对于模型的贡献程度情况