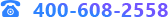【数学之美】分形——发现隐藏的维度
2020-11-07 09:12:17
次
仔细回想一下,在我们的生活中,无论是蜿蜒曲折的海岸线、绵延的山脊、变幻无常的云团,盘根错节的树根,还是人体的毛细血管,尽管它们的形状是不规则的,但如果用不同倍数的镜头来观察,它们的局部、分支和整体都有着非常高的相似性。
数学家们将这种“可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状“的形态特征叫做分形,最早由数学家曼德尔布罗特(B.B.Mandelbrot)在1973年提出。
尽管上述自然现象中的分形可能不那么完美,但是一旦我们利用数学公式,就可以构造出各种各样的完美分形。
数学里的分形
数学里的分形可以说是从康托尔集(Cantor Set)开始的。一个线段把中间的1/3去掉,得到两个分开的线段,再对剩下的两段进行相同的操作,得到4个线段。这样重复进行下去直到无穷,最后得到的图形集合就是康托尔集。用一个看似简单的步骤得到了一个无限复杂的图形,而且它的每一个细节放大之后都和整体看起来一模一样。
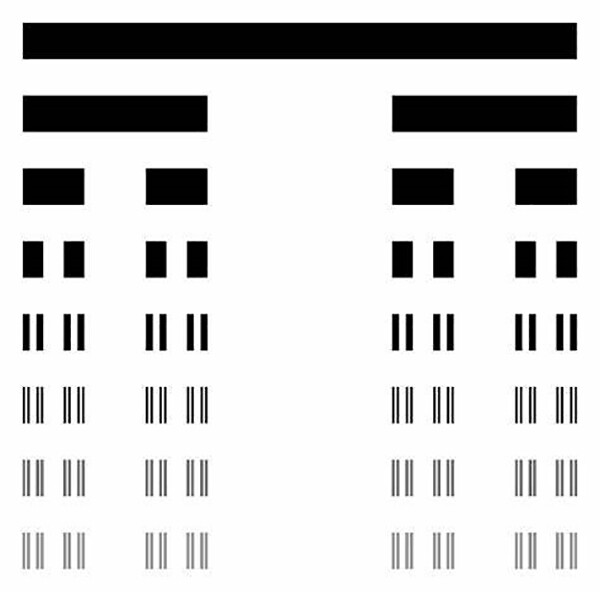
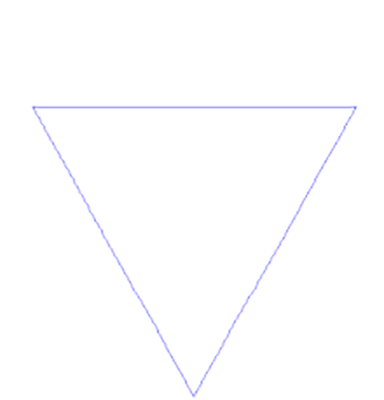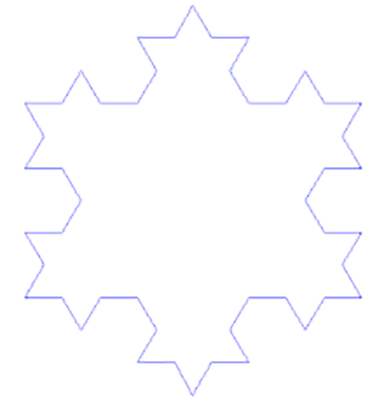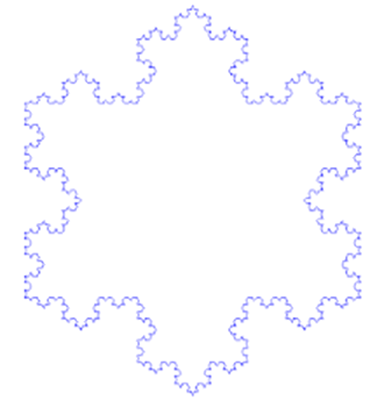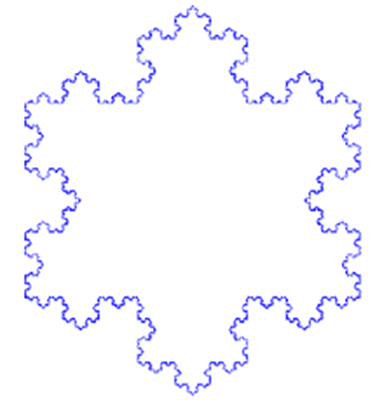
科克曲线(Koch snowflake)从一个正三角形开始,在它的每个边上增加一个1/3大小的小三角,它就变成了一个六角星,接着在每个小三角的边上继续增加它的1/3大小的小三角,然后无限重复这个过程。就会得到一个看上去像是雪花的图形。
如果说康托尔集是最平淡的分形,那么科克曲线才真正展示了分形之美。当你放大之后,就会发现它的每一个边都是自身形状的无数次重复。不仅如此,这个图形还有一个神奇的特性:它有着无限长的边长,但是它的总面积却最大不会超过雪花的外接圆面积。换句话说,一根无限长的曲线围住了一块有限的面积。
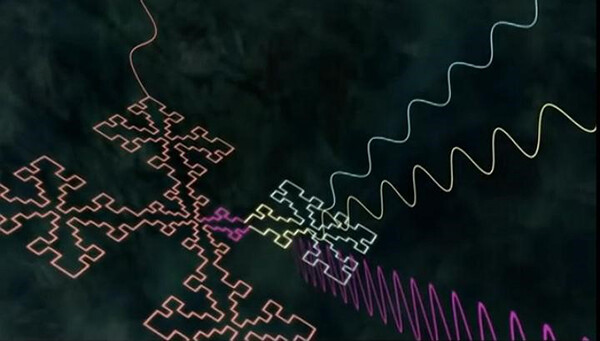
一个更有代表性的分形图案:皮亚诺曲线(Peano Curve)。一根线不断构造自相似的形状,最终把正方形填满。这样一条本该是一维的曲线却凭借分形特征填满了二维的形状,似乎已经超越了一维的境界,但说它是二维图形又还不够。那它到底是一维还是二维呢?
曼德勃罗特集(mandelbrot set)以分形之父曼德尔布罗特的名字命名,可能是人类有史以来做出的最奇异,最瑰丽的几何图形,曾被称为“上帝的指纹”。它集非常简单的产生公式和无限复杂的图像为一体。有的地方像日冕,有的地方像燃烧的火焰,只要计算的点足够多,不管你把图案放大多少倍,都能显示出更加复杂的局部。这些局部既与整体不同,又有某种相似的地方,好像有无穷无尽的细节和自相似性。
类似有趣的分形还有很多,我们一起来看些例子吧。
分形的应用
我们身边充斥着无处不在的分形,同时,我们也将分形的概念和方法应用在诸多领域。
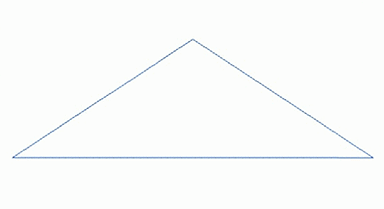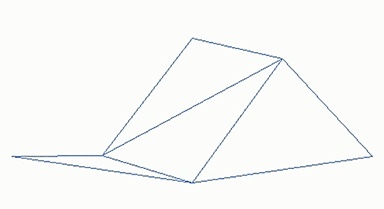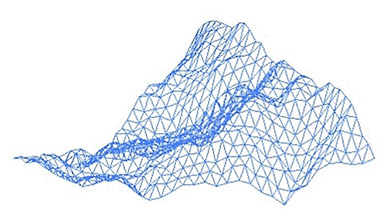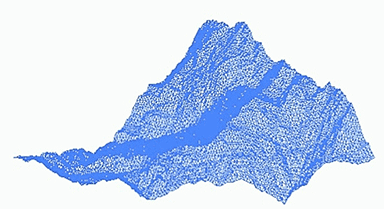
美国皮克斯公司的创始人之一、计算机科学家洛伦·卡彭特,用分形理论第一次在电脑绘制出让人瞠目的3D山峦巨石。从一个全景图出发,由一些非常粗略的三角形构成,然后对于每个三角形,分成4个小三角形,继续这样迭代,最终形成了非常逼真的山脉。这一方法成为了现在电影、游戏中实现特效的重要方式。
在无线电领域,如果你观察用于信号接收的天线,你会看到优美的自相似分形。通过分形设计让线路在狭小的空间内无限扩展(工艺允许的情况下)长度,不仅大大缩小天线的体积,还可以保证更好的收发效果。也正是因为分形的应用,我们的手机才得摆脱了那些明显的天线,做成现在这种精致的样式。
美国PBS电视台于2008年制作了一部名为《寻找隐藏的维度》的数学纪录片,上述关于分形的所有内容都将在这部纪录片里得到更加生动地介绍。如果你对分形已经有了好奇,就赶紧点击观看吧!
观看链接:https://www.bilibili.com/video/av15972423