Menu
美林数据立即试用申请试用
美林数据方案咨询方案咨询
美林数据
ABOUT US
美林数据技术股份有限公司（简称：美林数据，NEEQ：831546）是国内知名的数据治理和数据分析服务提供商。

产品简介

相关推荐

Tempo+金融|银行智能分析决策平台建设实践 Tempo+金融|银行智能分析决策平台建设实践
数字化转型的四大典型场景，TempoBI来支持 数字化转型的四大典型场景，TempoBI来支持
数据分析上手难？2招帮你快速生成高质量数据可视化报表 数据分析上手难？2招帮你快速生成高质量数据可视化报表

美林新闻/NEWS

首页 美林数据 大数据分析与应用

大话数据挖掘之聚类分析（上篇）

2021-01-28 14:17:45 次
人物介绍
许教授：国内数据挖掘专家、某985高校智能信息处理学术带头人
赵总：某电力公司总经理
万总：某超市集团营销副总
姜局长：市卫生局副局长
李部长：某钢铁集团生产部部长
 
某985高校管理学院第五届EMBA班的《数据挖掘及其应用》课程上。
国内数据挖掘专家、智能信息处理学术带头人徐教授站在讲台上打开PPT说：“同学们，大家好！今天我们讲的是数据挖掘中的聚类分析。”
“在平时的人际交往和私下的生活空间中，大多数人会自觉不自觉地加入到一个个社交圈子中。‘驴友’、‘同学会’、‘高尔夫俱乐部’，林林总总。真可谓‘物以类聚，人以群分’。”徐教授开始了聚类的讲解。

聚类算法

“徐老师，是不是说，圈子就是聚类？”一学员问。
徐教授没有正面回答，继续说：“大家想一想，生活中的圈子有什么特点？”
李部长说到：“社会学家指出，‘圈子’就是由志向、趣味、地位、年龄、职业、爱好、特长、个性、收入甚至居住地点比较相近的人自发形成的团体。”
“对了，正是因为这些人具有相似的特征，他们才能聚集在一起。聚类就是将数据对象划分成若干个类，在同一类中的对象具有较高的相似度，而不同类中的对象差异较大。”徐教授趁机给出了聚类的经典定义。
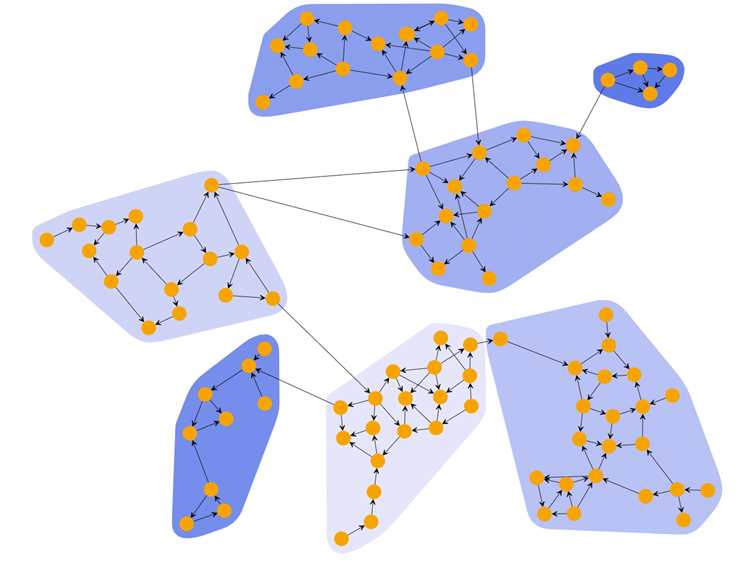
机器学习-聚类算法

刚才提问的那位学员从徐教授话语悟出了聚类的真谛，感慨道：“我有点明白了，我们加入某个‘圈子’，实际上就是聚类的过程，因为这个圈子的成员与我们有着相似的特点。”
这时，徐教授才对这位学员理解的圈子就是聚类作了正面回应：“回答正确，加十分！”
“徐老师，从聚类的定义来看，进行聚类前并不知道所研究的对象有多少个类，聚类的过程就是通过相似性的度量，使对象聚集成若干个类，各个类的成员具有其共同的或相似的特性。”李部长说出了自己对聚类的理解。
徐教授认为李部长的理解已经比较深刻，频频点头。他因势利导，又提出了一个深刻的问题：“聚类的关键是对象相似性的度量，大家想一想，如何度量数据对象的相似性呢？”
李部长抢答道：“两个对象间的距离越小，说明二者越相似，用距离度量对象的相似性应该是最自然的方法。”
徐教授满意地点了点头：“对，基于距离度量对象的相似性的思想，研究者提出了两类经典的聚类算法：划分方法和层次聚类方法。”
赵总似乎对这两种方法有所了解，说道：“听我们公司数据挖掘算法组经常说Partitioning Method和 Hierarchial Method，原来就是指的这两类聚类算法。徐老师，昨天晚上我预习时大概了解了一下聚类算法，但理解的不够深刻，您就给我们讲讲吧。”
徐教授欣然答应，但没有立即开始讲算法，他先引导学员回顾基本的数学知识，问道：“大家还记得距离怎么计算？”
赵总简洁地答道：“用欧氏距离呗！”
“对，就是大家在高等数学中经常用到的欧几里得(Euclid)距离。不过在聚类分析中，还经常用到曼哈坦(Manhattan)距离、切比雪夫(Chebyshev)距离、马哈拉诺比斯(Mahalanobis)距离等。其实，凡是满足距离定义的四个条件即唯一性、非负性、对称性和三角不等式的函数都可以作为距离公式。”
徐教授扫视了一下学员，觉得大家理解了距离的含义，于是说：“好了，我现在就简单地介绍一下基于距离的聚类算法：划分方法和层次方法。这两类方法的典型代表分别为k-Means、k-Medoids和聚集、分裂算法。下面我就分别介绍这些算法。”
徐教授翻动了一下PPT，接着道：“k-Means算法的核心思想是把n个数据对象划分为k个类，使每个类中的数据点到该类中心的距离平方和最小。”
李部长的脑子是双核的，徐教授的话音刚落，他便道出了他的理解：“徐老师，k-Means算法本质上是在实现聚类的基本思想：类内数据点越近越好，类间点越远越好尽可能算法。”
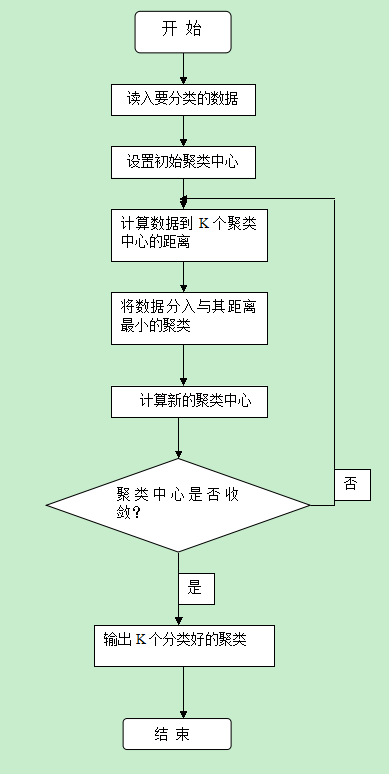
“李部长理解得完全正确，不过k-Means算法的思想只是给出了一个优化目标——距离之和最小，具体实现一般使用如PPT图示的迭代算法。”
学员们都将注意力集中在k-Means算法框图上，赵总看出了问题：“徐老师，k-Means算法事先就给定了聚类的个数k，然后通过迭代过程将数据点聚集到k个类中去。但是，一般情况我们并不知道数据点可以聚集成多少个类。”
“赵总说的对，k-Means算法就是要尝试找出使平方误差函数值最小的k个划分，为了找出最合适的聚类个数k，一般要用若干个k去试验，哪个k最后得到的距离平方和最小，就认为哪个k是最佳的聚类个数。”徐教授回答说。
李部长问道：“徐老师，k-Means算法第(3)步中的聚类中心是怎么计算的？”

聚类算法
 
“很简单，将已聚集的点的均值作为新的聚类中心。这正是将这种聚类算法成为k-Means算法的原因。如果以各聚类均值点最近的点为聚类中心，其他步骤不变，则k-Means算法就变为k-Medoids算法了。”徐教授回答道。
徐教授突然冒出了个k-Medoids算法，又被李部长的双核脑筋捕捉到了：“徐老师，k-Medoids算法只是对k-Means算法作了个小小的改变，这样有什么作用呢？”
徐教授笑了笑，说：“k-Medoids算法用簇中最靠近中心的一个对象来代表该簇，而k-Means算法用质心来代表簇。可见k-Means算法对噪声和孤立点数据非常敏感，因为一个离群值会对质心的计算带来很大的影响。而k-Medoids算法通过用中心点来代替质心，可以有效地消除这种影响。”
听徐教授这么一解释，李部长又大发感慨：“真是小改变，大作用啊！”
赵总觉得他们电力行业对数据挖掘有迫切的应用需求，非常关注算法的应用效果，又问道：“k-Means算法的应用效果怎么样？”
徐教授：“当结果簇是密集的，而簇与簇之间区别明显时，k-Means算法的效果较好。对于大规模数据集，该算法是相对可扩展的，并且具有较高的效率。
李部长不仅脑子转速高，而且善于从反面思考，他又提出了一个问题：“徐老师，k-Means算法和k-Medoids算法有哪些不足呢？”
徐教授对答如流：“首先，k-Means算法和k-Medoids算法只有在簇的数据点的平均值有定义的情况下才能使用。这可能不适用于某些应用，例如涉及有离散属性的数据。”
还没有等徐教授的“其次”出口，一直只听不说的超市集团的万总，被徐教授的这句话触动了，道出了她们数据挖掘时遇到的问题：“k-Means算法和k-Medoids算法一般适用于连续变量，而对于离散属性的对象，例如两本书，A=(小说，英文，1/32开本，浙江大学出版社)，B=(计算机图书，中文，1/16开本，浙江大学出版社)，就无均值可言，当然无法使用这两种算法。那么，对于含有离散属性数据的聚类问题怎么办呢？”
徐教授：“为了就解决这类问题，人们对k-Means算法进行改进，出现了很多它们的变种，例如，k-模算法用模代替簇的平均值，用新的相异性度量方法来处理分类对象，用基于频率的方法来修改聚类的模。而k-Means算法和k-模算法相结合，用来处理有数值类型和分类类型属性的数据，就产生了k-原型算法。”
听了徐教授的回答，万总非常高兴：”k-模算法和k-原型算法对我们可太有用了。徐老师，您就详细给我们讲讲k-模算法和k-原型算法吧！”
徐教授看了看手表，说道：“今天的时间差不多了，关于k-模算法和k-原型算法的更多内容我们下节课再讲。同学们，下节课见！”
上一篇：数据驱动业务，构建制造型企业新型能力 下一篇：大数据时代，还在用老一套方式管理采购与供应商吗？

联系我们

全国服务电话：

400-608-2558    029-8869-6198

企业邮箱：tempo@meritdata.com.cn

地址：中国西安 ▪ 雁塔区西三环天谷八路软件新城国家电子商务示范基地六层

  • 扫码关注我们

  • 扫码立即咨询

友情链接：美林数据官网　　　Tempo Talents大数据应用能力成长平台
Copyright © 2020 MeritData.All Rights Reserved 陕ICP备05005361号-1.    陕公网安备 61019002000171号
网站地图
版权所有@2022 美林数据技术股份有限公司
服务热线
400-608-2558
咨询热线
029-88696198
美林数据
微信扫描二维码，立即在线咨询